When one task is too difficult or time consuming to be done by one person, people form a team and work together to achieve a common goal. This is not just important for everyday life, but also for businesses and their employees. Teams have been recognized as critical to business success for some time. It is important that people not only form teams, but also that these teams are effective. Much work has been done to develop methods to help team members work more effectively on their own as well as with the group. Some methods such as agile software development and the Scrum framework place a particular focus on working rapidly to complete small goals. Many focus on qualitative studies of teamwork and success, but do not gain the insights that are inside the vast data available.
With modern developments in computational power and the increasing availability of large datasets, researchers are now able to apply quantitative methods to the study of teams, not just relying on small case studies. People are even using technology to put together large teams to solve problems in mathematics and computer science. We are particularly interested in the temporal patterns which emerge from how people do work. Anecdotally, we would imagine that people do work in a fairly “bursty” manner. Someone might work for a few days on a project, not touch that project for several weeks, and then work on it for a few more days on end. This idea of burstiness is, in fact, quantified by researchers which allows us to analyze whether people actually do work in a bursty manner, as well as the bearing it may have on their success. Alongside burstiness is another measure as well, called the memory coefficient, and this value measures the degree to which the time since the last event influences the time until the next one. These metrics have been used by many researchers to study such things as edit wars on Wikipedia and gene activity in E. coli. Bursty signals have been observed in many types of human behavior including emails, library loans, printing, and telephone calls.
GitHub is now the leading online platform for open source software development. For public projects, all activity related to the project is publicly available, including when contributions are made, when team members are added, and when general users interact with the repository. In this study, we build off of the work of Klug and Bagrow here by utilizing GitHub activity data to analyze whether people work in a bursty manner. We present the results of analyzing more than 150,000 teams, looking not only at whether teams exhibit burstiness, but also whether burstiness is correlated with success. This gives insights into ways to structure teams so that success can be maximized.
Interevent distributions
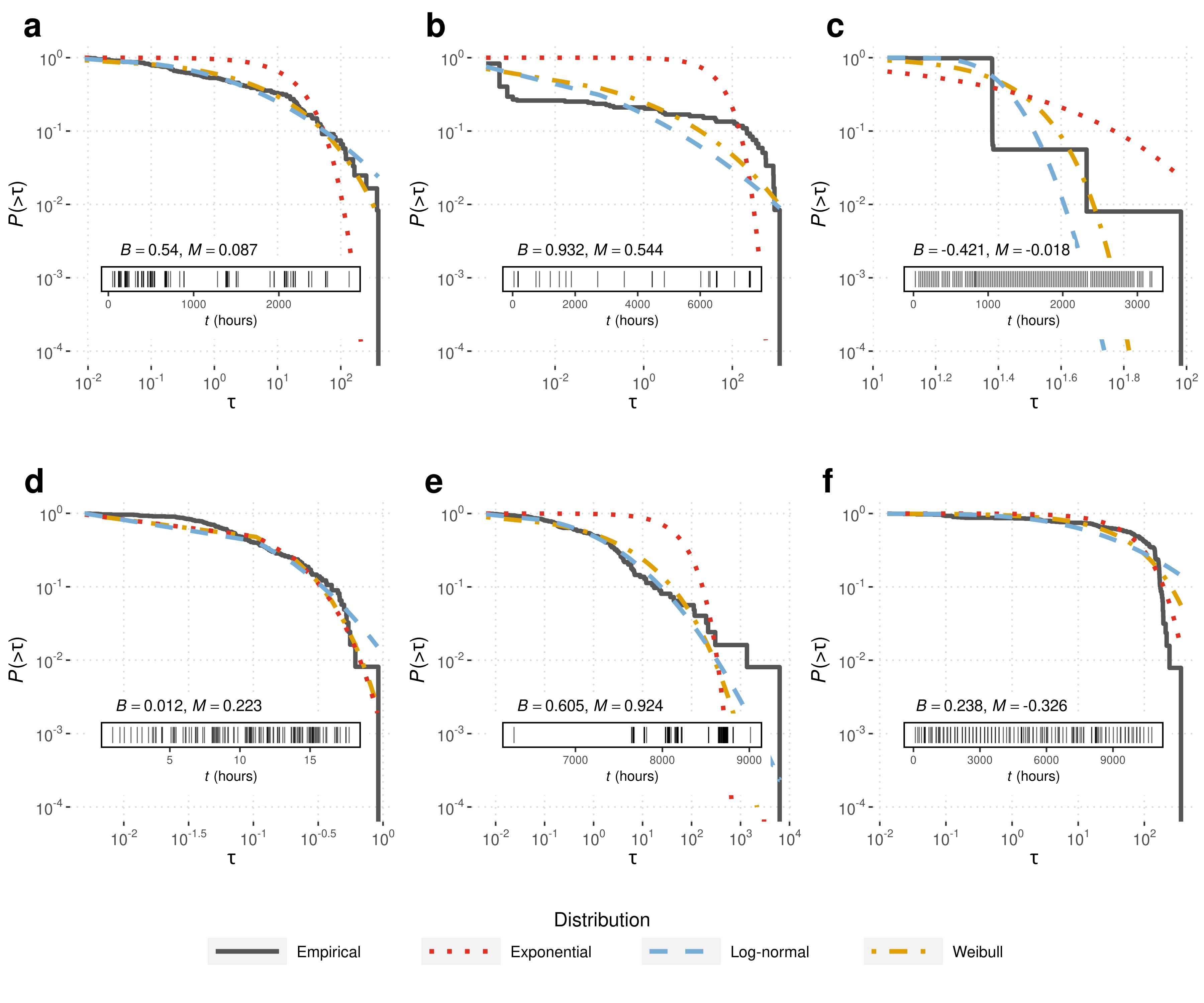
Formal measures of burstiness and memory, defined by Goh and Barabasi here are based on measures related to the distributions of times between certain events. In our work, the events are individual commits to GitHub repositories, and thus we are interested in the distributions of the times between these commits. Based on findings of other past works, we considered using the exponential distribution, the log-normal distribution, and the weibull distribution. The figure below shows the results of fitting each of these distributions to six different repositories’ interevent times. The solid dark gray line shows the empirical distribution, and the color lines represent the three different distributions. The insets in each subfigure also show the time series of each repository’s activity. With some of the repositories, both the log-normal and Weibull distributions fit quite well (a, d, d, f), but with others (b, c) the distributions offer very poor fits. The exponential fits are also included to show what a random interevent distribution would look like.
Picking a distribution
Based on the results of the analysis described above, as well as results from complementary analyses led us to choose the Weibull distribution for our data. The log-normal and the Weibull distributions both fit the data well, but we ended up choosing the Weibull distribution over the log-normal because it did a much better job of differentiating between different repositories.
Burstiness parameter B
The burstiness paramater as defined by Goh and Barabasi is a parameter that ranges from −1 to 1, with negative values indicating anti-bursty behavior, 0 random behavior, and positive values indicating bursty behavior. For example, in the figure above, (a) is moderately bursty, (b) is extremely bursty, and (c) is moderately anti-bursty. This parameter can be computed empirically from the data (displayed in the insets of the above figure), but we are more interested in computing it based off of the distribution we fit to the data. It is defined in terms of the coefficient of variation of said distribution.
Memory coefficient M
The memory coefficeint is essentially the pearson correlation coefficient between the set of interevent times and the set of interevent times offset by one position. It looks at how closely related a given interevent time is to the one that follows it. M, like B, ranges from −1 to 1, with positive values indicating that short interevent times tend to be followed by a short one, and negative values indicating that short interevent times tend to be followed by long ones. Examples of different values of M can be seen in Figure 1. Subfigures (a) and (c) have M close to 0, (b) and (d) have moderately positive values of M, (e) has a very positive value of M , and (f) has a fairly negative value of M.
Joint distribution of B and M
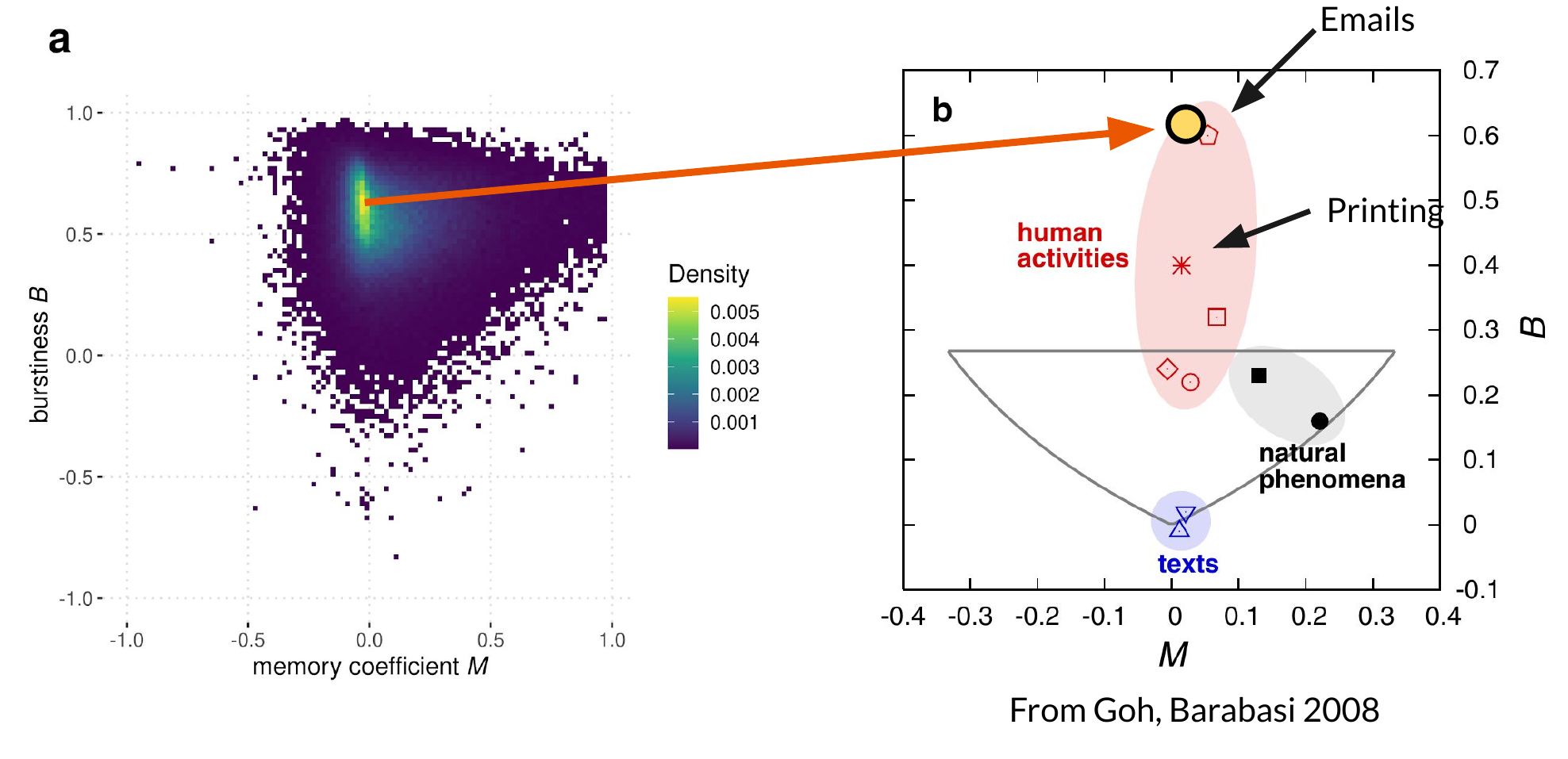
With a distribution selected and B and M defined in terms of paramters of the fit distributions to each set of interevent times, we can now fit a distribution to each repository’s set of interevent times using maximum likelihood estimation, and then we can compute B and M based on measures of that fit distribution. Doing so yields us a joint distribution of B and M for all repositories, shown in subplot (a) of the figure below.
Subplot (b) is taken from the study by Goh and Barabasi referenced earlier, which shows the modes of the joint distributions of B and M for other types of data such as emails, printing, and natural phenoma. Mapping the mode of our measures to the same subplot (displayed as a yellow circle) shows that peoples’ work on GitHub exhibits similar burstiness and memory characteristics to that of people sending emails, which is a reasonable result.
Relating burstiness and memory characteristics to the success of a team
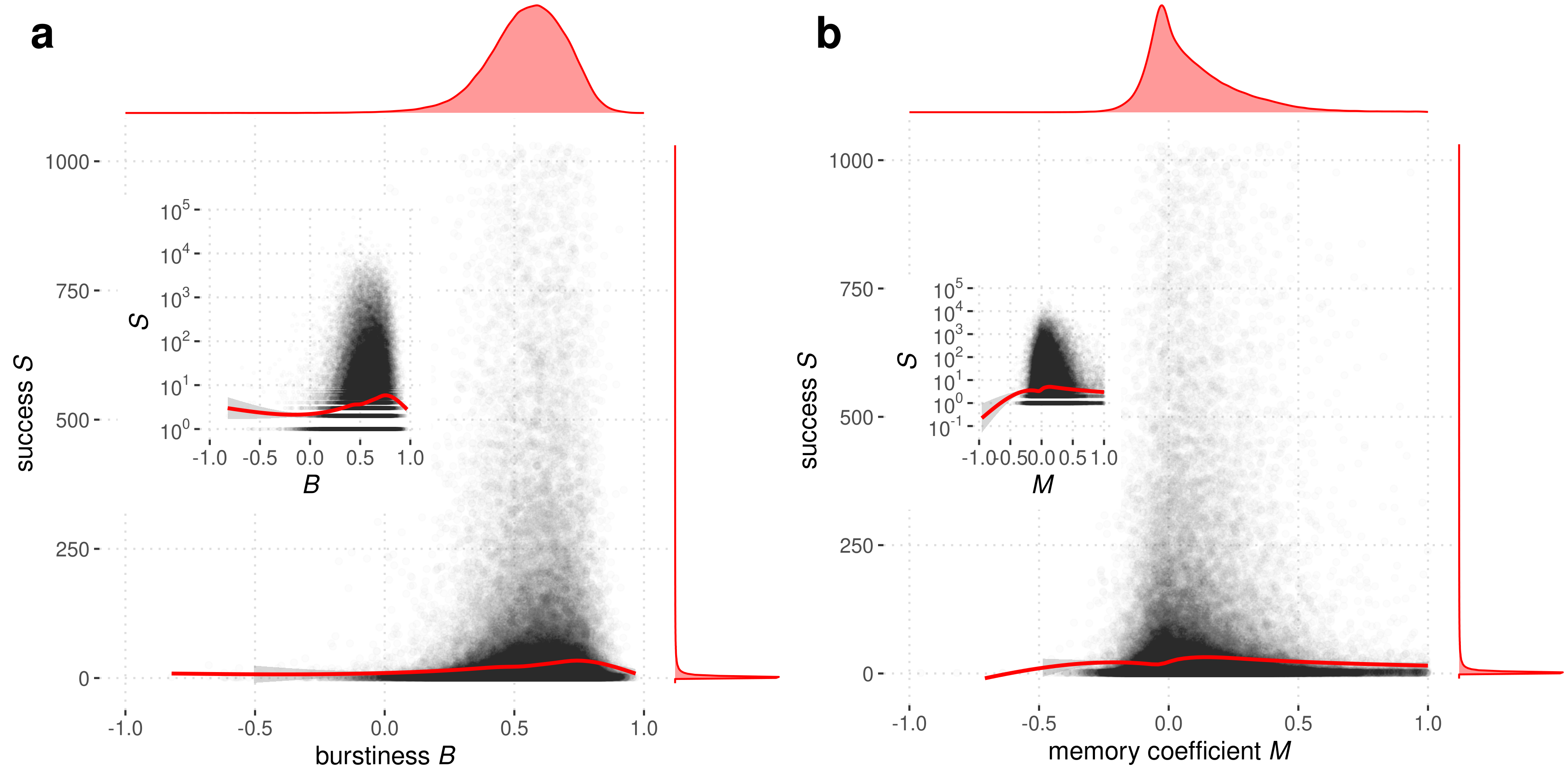
One of the additional pieces of information we have about each repository in the study is the number of stars it received from users on GitHub. This can be viewed as a metric of success, as the act of starring a repository indicates a user’s interest in said repository. The figure below shows bivarate associations between success and burstiness(a), and success and the memory coefficeint (b).
Main plots of each subfigure show a scatterplot of the two variables along with a smoothed spline. Outliers (above the 99th percentile in S) were filtered out of the main plot. Margins show the one-way distribution of each variable. Insets show the same scatterplot and smoothed spline on a logarithmic scale, this time including outliers. There is a slight postive association between S and B, and it is more evident on the logarithmic scale. Based on the splines in (a), higher values of B are associated with higher values of S, to a point. Slightly positive values of M are associated with greater values of S, but the association is minimal.
The association seen visually here, while minimal, is statistically significant as supported by an additional analysis of fitting regressing a repository’s number of stars on B, M, and many other key characteristics of the repositories.
Conclusions
Teams on GitHub certainly exhibit bursty behavior. The degree of teams’ burstiness falls in line with other human activities, specifically printing and emailing. Because the overall burstiness of the teams falls in line with other human activities, it means that we have shown that groups of people act in similar patterns to individuals. This pattern of burstiness could be explained by social loafing, as teams could fall in and out of complacency when many people are working on the same team.
When beginning this project, we were hoping to see a much stronger association between par- ticularly burstiness and success than we did. Instead, we found the opposite: teams are able to, for the most part, find success regardless of how bursty or memory-dependent their work patterns are. A more in depth analysis in the future could investigate interevent times grouped by both team and team member. This has its own set of challenges, as more bias would be introduced due to the notable increase in filtering that smaller subdivisions requires.
If you are interested in more details and specifics of this study, I encourage you to check out the repository containing full paper, a slide deck, and code located here.